在一次面试当中，面试官问到了自己关于堆排序的一些细节，之前在整理各种高级排序的时候，有看过堆排序，然而在现场要给面试官讲解排序的原理的时候，发现自己懵逼了，所以还是需要特地写一篇随笔来记录堆排序的整个原理和过程，这里借鉴了百度知道里头的堆排序的讲解图。

　　首先我们要了解什么是堆排序，其排序的时间复杂度为O(nlogn)，且不会因为排序的数组的数据恶化，但需要提供额外的排序内存。这里的堆当中，常用的数据结构就是二叉树，且是完全二叉树。根据要排序的方式（升序，降序）可以将这个二叉树的特点定义下来，就是根节点都比左右子节点大（大根堆）或者是根节点都比左右子节点小（小根堆）。而整个堆排的过程，包括了一个建树，调整树顶的过程。二话不说，先举一个例子来说，假定我们要对序列{16,7,3,20,17,8}进行排序，先上我们的流程图：

这是初步构建出来的树，之后，我们从叶子节点开始从底向上遍历，调整树当中的数据，使其成为大根堆：

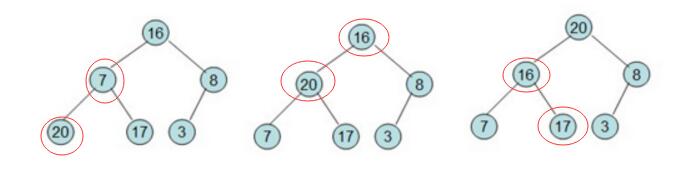
通过对图中画红圈的节点进行数据交换，我们可以得到构建出来的大根堆：

之后我们将根节点和最后一个叶子节点互换，并且将互换后的这个叶子节点固定住（表示这个点已经被排序好）之后调整树的时候不对该再进行调整。

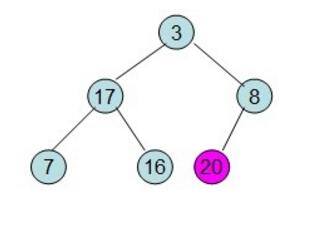
之后的过程依次类推，最后就可以得到一个排序好的数组。

整个流程通过图可以看的很清晰。那么接下来我们来看看代码实现：

public class testHeapSort {    public static void main(String[] args) {        // TODO Auto-generated method stub        int[] input={2,3,5,2,3,6,7,4,6};        HeapSort(input);        for(int tmp:input)            System.out.print(tmp+" ");    }        //堆排序    public static void HeapSort(int array[])    {        buildTheTree(array);                //从数组当中最后一个位置开始固定，一次固定到头，即可得到升序数组        for(int i=array.length-1;i>=1;i--)        {            //根和当前最后的叶子节点交换            int tmp=array[0];            array[0]=array[i];            array[i]=tmp;                        //调整堆            maxify(array, i, 0);        }    }        //第一次建树    public static void buildTheTree(int array[])    {        //因为是从叶子节点开始从底向上的调整，所以起点为数组长度的2分之一        int half=array.length/2;                for(int i=half;i>=0;i--)        {            maxify(array, array.length, i);        }            }        //调整树的方法，大顶堆    public static void maxify(int array[],int size,int i)    {        //左子节点        int left=2*i+1;        //右子节点        int right=2*i+2;                //找出当前根节点、其左子节点、右子节点最大的节点作为根节点        int large=i;        if(left
     
      array[i])large=left;        if(right
      
       array[large])large=right;                //如果再上边查找过程当中，根节点就是最大的节点，那么不需要再去调整树，因为这是一个从下往上调整的过程        //所以当前节点以下的树已经满足大根堆的要求，直接返回        if(large==i)return;                //如果需要当前根节点和子节点互换，则互换过去的子节点再一次调整        int tmp=array[large];        array[large]=array[i];        array[i]=tmp;        //互换后调整。        maxify(array, size, large);    }}
      
     

通过代码当中的注解，结合流程图应该就可以很清晰的理解堆排序的原理和实现过程，这里就不再进行赘述了。